Group Relative Policy Optimization

An efficient and effective reinforcement learning algorithm

While everyone is excited about DeepSeek-R1, we'll focus on discussing the reinforcement learning algorithm used by its junior model, namely DeepSeek-R1-Zero. The algorithm is known as Group Relative Policy Optimization (GRPO) and, in a certain sense, is an evolution of the PPO algorithm.

The Proximal Policy Optimization algorithm

Proximal Policy Optimization (PPO) is an algorithm that aims to improve the stability and efficiency of policy gradient methods. PPO optimizes the policy directly by maximizing an objective function while ensuring that the policy update doesn't deviate too much from the previous one. This prevents drastic updates that could lead to instability in training, a problem that is common in policy gradient methods. PPO is widely used in the RL fine-tuning stage of LLMs and it optimizes LLMs by maximizing the following surrogate objective

\(\displaystyle \mathbb{E}\left( \frac{1}{\mid o \mid}\sum_{t=1}^{\mid o \mid} \min \left[ r_tA_t, \mathrm{clip}(r_t, 1-\epsilon, 1+\epsilon)A_t\right]\right)\)

where

• the expectation is on questions q sampled from the question dataset and outputs o sampled from the old policy π_θold;

• the term

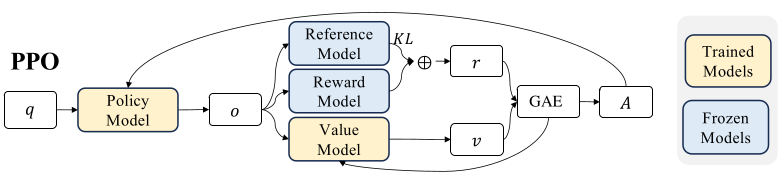
  \(\displaystyle r_t = \frac{\pi_\theta (o_t \mid q, o_{<t})}{\pi_{\theta\mathsf{old}} (o_t \mid q, o_{<t})}A_t\)

  is the ratio between the new and the old policy multiplied by the advantage A_t;

• if we blindly maximize r_t, it may lead to a very large update to the policy weights, so a clip term is used for the objective to limit the ratio between the new and the old policy to be in the interval [1 − Є, 1 + Є];

The advantage function A is is the difference between the action-value function of a determined action a in state s and the state-value function of state s under a determined policy π and describes how much better it is to take action a instead of following policy π - that is, the advantage of choosing action a over the default action. For PPO the advantage A_t is computed by applying Generalized Advantage Estimation (GAE, check the Supplementary Material, section A, of this paper for more).

The advantage function A_t evaluation is based on the rewards { r_>t } and a learned value function 𝑉𝜓 (the baseline). Thus, in PPO, a value function needs to be trained alongside the policy model. This value function is generally another model of similar size to the policy model, which significantly increases both memory usage and computational demands. A per-token KL penalty (depending on a reference model) is added to mitigate over-optimization of the reward model. Everything is summed up in the following figure.

Furthermore, In LLMs, the reward (like a grade) is usually given only for the final output, not for each word/token. This makes it tricky to train a reliable value function (the helper that estimates how good each step is), because there’s no clear signal for individual parts—only the whole result. It’s like trying to bake a perfect cake but only getting told if it’s good or bad at the end, with no clues about which ingredients or steps mattered.

The GRPO approach

We just said that training a baseline value model would be impractical. Hence, to obviate the need for additional value function approximation as in PPO, the GRPO strategy provide sampling multiple outputs from the old policy for the same question or state and treating the average reward of these outputs as the baseline. Anything above average yields a positive advantage. Similarly to PPO, GRPO retains Clip and KL terms to ensure stable updates.

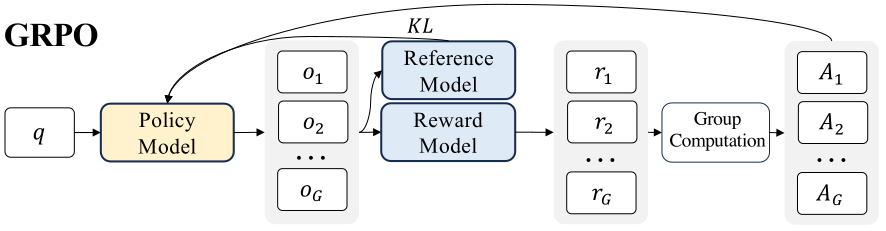
for each question q, GRPO samples a group of outputs { o₁ , o₂ , · · · , o_G } from the old policy π_old and then optimizes the policy model by maximizing the following objective

\(\displaystyle \mathbb{E}\left( \frac{1}{G}\sum_{i=1}^{G} \frac{1}{\mid o_i \mid}\sum_{t=1}^{\mid o_i \mid} \left\{ \min \left[ r\,A, \mathrm{clip}(r, 1-\epsilon, 1+\epsilon)\,A\right]- \beta\, \mathrm{D}\right\} \right) \)

where epsilon and beta are two hyper-parameters, the expectation is taken with respect to questions q and samples { o₁ , o₂ , · · · , o_G }. The ratio r = r_i,t is

\(\displaystyle r_{i,t} = \frac{\pi(o_i)}{\pi_{old}(o_i)}\)

and D is the KL-divergence term KL( π || π_ref ) measuring the difference between the model policy and the reference model policy (ref model discourages “cheating” or extreme deviations).

Now, the advantage A = A_i,t can be evaluated either focusing on the final result (the end outcome) or through the intermediate steps (the process) leading to the goal. For the outcome, for each question q, a group of outputs { o₁ , o₂ , · · · , o_G } are sampled from the old policy model π_old . A reward model is then used to score the outputs, yielding G rewards r = {r₁ , r₂ , · · · , r_G } correspondingly. Subsequently, these rewards are normalized by subtracting the group average and dividing by the group standard deviation. So

\(\displaystyle A_i = \frac{r_i - \mathsf{mean}(\{r_1, r_2, \dots, r_G\})}{\mathsf{std}(\{r_1, r_2, \dots, r_G\})}\)

For the process, there is a quite obvious way to provide a reward at the end of each reasoning step: consider several sets of G rewards (a set for each step of the process) and considering a similar quantity A as before.

All this is encompassed in the following figure.

Conclusion

GRPO removes the need for a separate value network in LLMs, reducing memory and computation costs. GRPO should enhance reasoning abilities while concurrently optimizing the memory usage of PPO.

---

Useful links

DeepSeekMath paper (link)

DeepSeekR1 paper (link)

DeepMimic (link)

DeepSeek-R1 Dissection: Understanding PPO & GRPO Without Any Prior Reinforcement Learning Knowledge (link)

---