LLMs: a 5 mins trip

What Large Language Models actually do in mathematical terms

Large Language Models (LLMs) have revolutionized the way we interact with text, powering everything from chatbots to advanced translation systems. But beneath their impressive capabilities lies a rich mathematical foundation that drives their understanding and generation of language. In this quick math tour, we’ll explore the essential mathematical structure that underpin LLMs. Just an overview, without delving into details.

Discrete distributions

Think of a discrete distribution as a set of stems or spikes, as in the following picture, representing the probabilities related to some objects — in this case we represent how frequently the individual letters of the alphabet appear in English language texts.

The letter “E” is the one with the highest frequency, so it has the greatest probability of appearing in a text. The sum of all the spike probabilities is 1. We can also choose a representation with squares (size = probability).

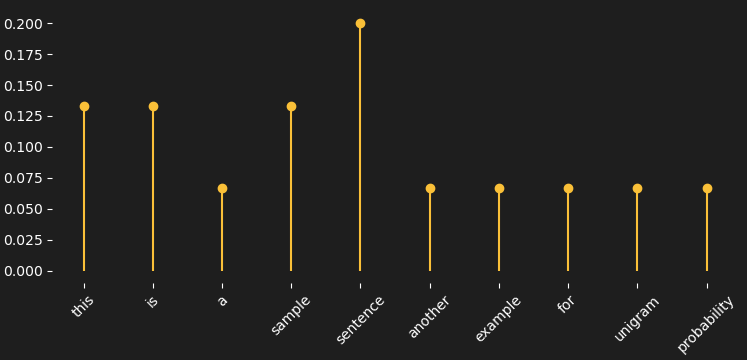
You can consider distributions over vocabularies. For example, consider the following toy corpus.

# Example - small corpus
corpus = [
    "this is a sample sentence",
    "this is another example sentence",
    "sample sentence for unigram probability"
]

The distribution associated to this simple example corpus is the following.

Large Language Model overview

Large Language Models (LLMs) are typically based on the Transformer architecture and employ an autoregressive approach. Autoregressive modeling in LLMs means that the model generates text one token at a time, predicting the next word based solely on the sequence of previously generated words, without looking ahead.

A token in natural language processing (NLP) is a unit of text that serves as a basic element for language models to process and understand language. The exact nature of a token can vary depending on the model and tokenization method used (for example, BPE). Enter some text on this page to see how tokenization works.

Input sentences or prompts are tokenized into a sequence of discrete tokens

\(x = (x_1, x_2, \dots, x_n), \quad x_i \in V\)

where V is the vocabulary (the set of unique tokens — which can be words, subwords, or characters — that the model can recognize, understand, and generate during language processing).

The LLM processes x token by token to produce a sequence of logits

\(L_x = (\ell_1, \ell_2, \dots, \ell_n), \quad \ell_i \in \mathbb{R}^{S}\)

where S = |V | is the vocabulary size. Each logit vector ℓ_i is a very very long vector (one entry for each element in the vocabulary!) that represents the model’s prediction for the i-th token, given preceding tokens (from x₁ to x_{i - 1}).

These logits are not probabilities but scores that reflect the model's relative preference for each token before normalization. For each position i, applying the softmax function (softmax transforms the raw output scores into a probability distribution) to ℓ_i yields a probability distribution over the vocabulary:

\( p(\,\cdot \mid x_1, \dots, x_{i-1}) = \mathsf{softmax} \begin{pmatrix} \ell_{i\,1} \\ \ell_{i\,2} \\ \vdots \\ \ell_{i\,S} \end{pmatrix} \in [0,1]^{S} \;.\)

The distribution p is represented by a long probability vector whose j-th entry is the probability of the j-th token being the next predicted token. There are various sampling methods to determine the final prediction for the next token; the arguably simplest approach, known as greedy sampling, selects the token with the highest probability y_i .

For the last input token x_n, the logits ℓ_n give the probability distribution

\(p(\,\cdot\mid x) \in [0,1]^{S}\;,\)

representing the likelihood of each token inV being the next token after x. Once we have done with the input sequence x, we will end up with a sampled output sequence

\( y = (y_1,y_2, \dots, y_m)\,.\)

The probability distribution for generating the i-th token y_i , conditional on input x and prior outputs y_<i = ( y₁ , . . . , y_i-1 ), is

\(p(·|x, y_{<i} ) ∈ [0, 1]^{S} \,.\)

This distribution represents the model’s estimation of the next token based on the prompt and the sequence generated up to that point.

Example

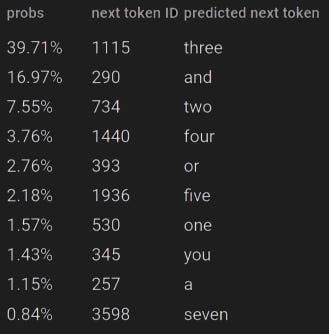
A language model like GPT-2 takes tokens as input and predicts the next token. Conceptually, this prediction can be seen as a multi-class classification problem, where each class corresponds to a possible token—in GPT-2’s case, there are 50257 such classes. For instance, given the sentence

One, two,

GPT-2 processes the token IDs [3189, 11, 734, 11] and assigns a 39.71% probability to the next token ID being 1115, which represents the token “three”.

Here probs represents — essentially, up to percentages — distribution p( · | x₁ , x₂ , x₃ , x₄ ). You can find more about the preceding example here.

Conclusions

So, under the hood, LLMs are next token prediction models. This is a controversial truth, which tends to belittle AI and fuels disillusionment among those who idealize an artificial intelligence with real reasoning abilities. But there would be too much to discuss about the relationship between human intelligence and the internal mechanics of AI models, certainly much more than the limited space dedicated to a simple blog.

---